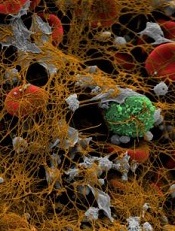
Image by Andre E.X. Brown
A group of biophysicists have developed a mathematical model of arterial thrombus formation.
The team described the process of platelet aggregation as being similar to the video game Tetris and derived equations that allowed them to reproduce the wave process of platelet aggregate formation in a blood vessel.
Mikhail Panteleev, PhD, of Moscow State University in Russia, and his colleagues described this work in PLOS ONE.
Looking at thrombus formation in the same way as the tiles stack up in Tetris is a key aspect of the team’s model. In the game, the tiles either drop down onto a flat surface or become attached to parts sticking out from the rest of the block.
The researchers said there are only 2 differences between thrombus formation and the game.
Unlike in Tetris, when a layer of a thrombus is complete, it does not disappear. So, as time passes, a thrombus is capable of obstructing the space it is in.
And Tetris includes tiles of several different shapes. But, in a thrombus, the “falling tiles” are always the same—thrombocytes.
Having described the mathematical process of how vacant areas on the surface of a growing thrombus are filled, the researchers were able to build first a 1-dimensional model (as in Tetris) and then a 2-dimensional model (where thrombocytes are deposited in a dimensional plane).
At one point, the researchers began to consider certain thrombocytes as being dimensionless and the thrombus itself as being continuous. In other words, they went from a discrete model to a continuous model.
In a discrete model, the system under study consists of individual particles, and the behavior of each particle can be tracked individually. In a continuous model, the system under study consists of solid objects that can freely change their size or any other characteristic.
The sequential solution of the equations enabled the researchers to reproduce the dynamics of thrombus growth and study clot behavior under various conditions—in the case of damage to the vascular wall, for example.
Active media and autowaves
The researchers said the process of thrombus formation is like an autowave. And the blood, which carries platelets and proteins for coagulation, is an active medium.
The term “active medium” plays a key role in non-linear dynamics—the science of mathematical modeling of a range of systems, from mixtures of interacting chemicals and lasers to forest fires and even social networks.
One way to describe an active medium is to use the example of a forest fire. Every dry tree is not simply a passive object but a potential source of thermal energy. If there is a fire near a dry tree, it too will start to burn and provide more heat, which can then ignite other trees. The ability of elements in the system to release energy is a key feature of an active medium.
In active media, a local event (lightning striking a tree, for example) can initiate a transition process in a system from one state to another (in this case, a dry tree becomes a burning tree).
This process spreads like a wave in space, and the specific physical nature of the system is not so important. The same equation can be used to describe entirely different cases.
The term “autowave” means the wave propagation process is not passive, as in the case of seismic waves traveling from an earthquake’s epicenter, but active. At each point, the wave receives more energy.
In the case of thrombus formation, these terms apply to thrombocytes flowing in plasma. The thrombocytes can go from a free-flowing state to a deposited state.
Under normal circumstances, thrombocytes flow freely in the bloodstream, but if the vascular wall becomes damaged, they start to adhere to one another and to the vascular wall.
The blood also contains proteins required for thrombus formation. Even if there are no thrombocytes, reactions with these proteins are able to help form a clot to block a damaged vessel, and these reactions also occur in the form of autowaves.
Normally, thrombi prevent blood loss in the human body when a blood vessel has become damaged. Sometimes, however, thrombus formation occurs not as a result of an injury with damage to a blood vessel, but as a result of a reaction to a pathological process.
This type of thrombus formation can block a vessel completely and cut off the blood supply to tissues and organs. This, in turn, can lead to myocardial infarction, stroke, or gangrene of the extremities.
The researchers say their new model correctly describes arterial thrombus formation. These particular thrombi consist mainly of thrombocytes, and blood proteins play a relatively small role in the process.
“We have always had difficulty working with arterial blood clots in particular, in terms of developing and implementing computer models, because the subject involves a very difficult combination of mechanics (cell attachments), hydrodynamics with variable geometry, and biochemistry,” Dr Panteleev said.
“In our paper in PLOS ONE, we tried to use the most primitive description of a thrombus as a continuous medium, rather than discrete particles. This approximation is rough in many respects, and it limits the scope of the research, but it is able to give us some common patterns.”
“On the one hand, we plan to continue to apply it to specific tasks, as far as is possible, and on the other hand, we are developing more sophisticated and advanced models with 3-dimensional blood cells, the full mechanics of their interaction, and the proper biochemistry.”